October 12, 2022
Coding & Algorithm Interview Data Structures & Algorithms
Introduction
I reviewed some implementations of the median function in widely used statistics packages. They use simple flow like sorting the array and returning the middle element.
The average runtime complexity of comparison-based sorting algorithms is linearithmic -> O(N log N)
And choosing the middle element is of constant runtime complexity -> O(1)
So the runtime complexity of this solution is still linearithmic -> O(N log N) + O(1) -> O(N log N)
Here, the question: ‘Is there any more performant solution to find the median of any unsorted array?’.
Yay, the good news is here. 🙂
The fundamental fact is that the problem is the type of selection problem and can be solved effectively with quicksort partitioning. What kind of efficiency might we expect in a selection algorithm? The lower bound complexity is O(N) because you have to look at every item. Our target will be achieving this lower bound as the upper bound.
3-way partitioning
We should have such a partitioning as below.

In the middle block, all the values are equal to the pivot value (v). All the values to the left are less than the pivot (< v), and all the values to the right are greater than the pivot (> v).
So, we have an array ARR of N elements. The leftmost index is 0 (lo), and the rightmost index is N – 1 (hi).
According to the median function definition:
- If N is odd, median value <- ARR[N / 2]
- Else If N is even, median value <- (ARR[N / 2] + ARR[N / 2 – 1]) / 2
Let’s keep K = N / 2
And our partition function returns the bounds of the middle block. -> [lt, gt]
So, after the partitioning phase is completed:
- If lt <= K <= gt, we are done, the median value is the pivot value, and the execution ends. For sure, if the N is even, there is a tricky part, you can find it in the code below.
- Else If K < lt, call the partition function for (lo, lt – 1) block
- Else If K > gt, call the partition function for (gt + 1, hi) block
From this perspective, this selection algorithm takes linear time on average. But why?
Each partitioning step splits the array approximately in half. N + N / 2 + N / 4 … + 1 ≈ 2 * N compares. The formal analysis yields ≈ 3.38 * N compares. But, we can say that they both have linear time complexity, just the constants are different, it does not affect theoric runtime complexity O(N).
An extremely important detail here is that quick select uses quadratic compares in the worst case. To protect ourselves from this unacceptable performance issue, we can shuffle the array or use Tukey’s ninther method to select the pivot element. In the below code part, we used the second one, it is more performant, with no need to shuffle all elements.
The Code
// https://serhatgiydiren.com
// Oct 12, 2022
#include <bits/stdc++.h>
using namespace std;
using namespace chrono;
mt19937 rng(steady_clock::now().time_since_epoch().count());
vector < int > orig;
struct bound
{
int left, right;
};
int median_index(vector < int > &arr, const int &i, const int &j, const int &k)
{
return ((arr[i] < arr[j]) ? ((arr[j] < arr[k]) ? j : (arr[i] < arr[k]) ? k : i) : ((arr[k] < arr[j]) ? j : (arr[k] < arr[i]) ? k : i));
}
void set_pivot(vector < int > &arr, const int &lo, const int &hi)
{
int n = hi - lo + 1;
if (n < 40)
{
int m = median_index(arr, lo, lo + n/2, hi);
swap(arr[m], arr[lo]);
}
else
{
int eps = n / 8;
int mid = lo + n / 2;
int m1 = median_index(arr, lo, lo + eps, lo + 2 * eps);
int m2 = median_index(arr, mid - eps, mid, mid + eps);
int m3 = median_index(arr, hi - 2 * eps, hi - eps, hi);
int ninther = median_index(arr, m1, m2, m3);
swap(arr[ninther], arr[lo]);
}
}
void insertion_sort(vector < int > &arr, const int &lo, const int &hi)
{
for (int i = lo; i <= hi; i++) for (int j = i; j > lo && arr[j] < arr[j-1]; j--) swap(arr[j], arr[j-1]);
}
bound partition(vector < int > &arr, const int &lo, const int &hi)
{
set_pivot(arr, lo, hi);
int i = lo, j = hi + 1;
int p = lo, q = hi + 1;
int pivot = arr[lo];
while(true)
{
while(i <= hi && arr[++i] < pivot);
while(j >= lo && arr[--j] > pivot);
if (i == j && arr[i] == pivot) swap(arr[++p], arr[i]);
if (i >= j) break;
swap(arr[i], arr[j]);
if (arr[i] == pivot) swap(arr[++p], arr[i]);
if (arr[j] == pivot) swap(arr[--q], arr[j]);
}
i = j + 1;
for (int k = lo; k <= p; k++) swap(arr[k], arr[j--]);
for (int k = hi; k >= q; k--) swap(arr[k], arr[i++]);
return {j, i};
}
double median_with_quick_select(vector < int > &arr)
{
int lo = 0, hi = arr.size() - 1;
int med_idx = arr.size() / 2;
double res = -1;
while(lo <= hi)
{
if (hi - lo < 8)
{
insertion_sort(arr, lo, hi);
if (arr.size() % 2) res = arr[med_idx];
else res = (arr[med_idx] + arr[med_idx - 1]) / 2.0;
break;
}
auto bounds = partition(arr, lo, hi);
if (med_idx >= bounds.right) lo = bounds.right;
else if (med_idx <= bounds.left) hi = bounds.left;
else // bounds.left < med_idx < bounds.right
{
if (arr.size() % 2) res = arr[med_idx];
else
{
if (med_idx == bounds.left + 1) res = (arr[med_idx] + *max_element(arr.begin(),arr.begin() + bounds.left + 1)) / 2.0;
else res = (arr[med_idx] + arr[med_idx - 1]) / 2.0;
}
break;
}
}
return res;
}
double median_with_sort(vector < int > &arr)
{
int len = arr.size();
double res = -1;
sort(arr.begin(), arr.end());
if (len % 2) res = arr[len / 2];
else res = (arr[len / 2] + arr[len / 2 - 1]) / 2.0;
return res;
}
void process()
{
int elapsed_quick_select;
int elapsed_sort;
map < pair < int , int > , int > cnt;
map < pair < int , int > , pair < long , long > > sum;
int run_count = 100000;
while(run_count--)
{
int cof = 3 + rng() % 6;
int array_size = int(pow(10, cof));
int random_max = int(pow(10, rng() % (1 + cof)));
orig.resize(array_size);
for(auto &e:orig) e = rng() % random_max;
clock_t c_start = clock();
auto arr_for_qsel = orig;
auto med_qsel = median_with_quick_select(arr_for_qsel);
elapsed_quick_select = clock() - c_start;
c_start = clock();
auto arr_for_sort = orig;
auto med_sort = median_with_sort(arr_for_sort);
elapsed_sort = clock() - c_start;
assert(med_qsel == med_sort);
pair < int , int > key = {orig.size(), random_max};
cnt[key]++;
sum[key].first += elapsed_quick_select;
sum[key].second += elapsed_sort;
cout << run_count << " : " << orig.size() << "," << random_max << "," << elapsed_quick_select << "," << elapsed_sort << " " << elapsed_sort * 1. / elapsed_quick_select << endl;
}
cout << endl << "========================================" << endl;
for(auto [key,val]:sum) cout << key.first << "\t" << key.second << "\t" << cnt[key] << "\t" << val.first / cnt[key] << "\t" << val.second / cnt[key] << "\t" << val.second * 1. / val.first << endl;
}
void fast_io()
{
ios::sync_with_stdio(false);
srand(time(NULL));
cin.tie(0);
cout.tie(0);
cout << fixed << setprecision(2);
cerr << fixed << setprecision(2);
}
int main()
{
fast_io();
process();
return EXIT_SUCCESS;
}Performance Comparison Results
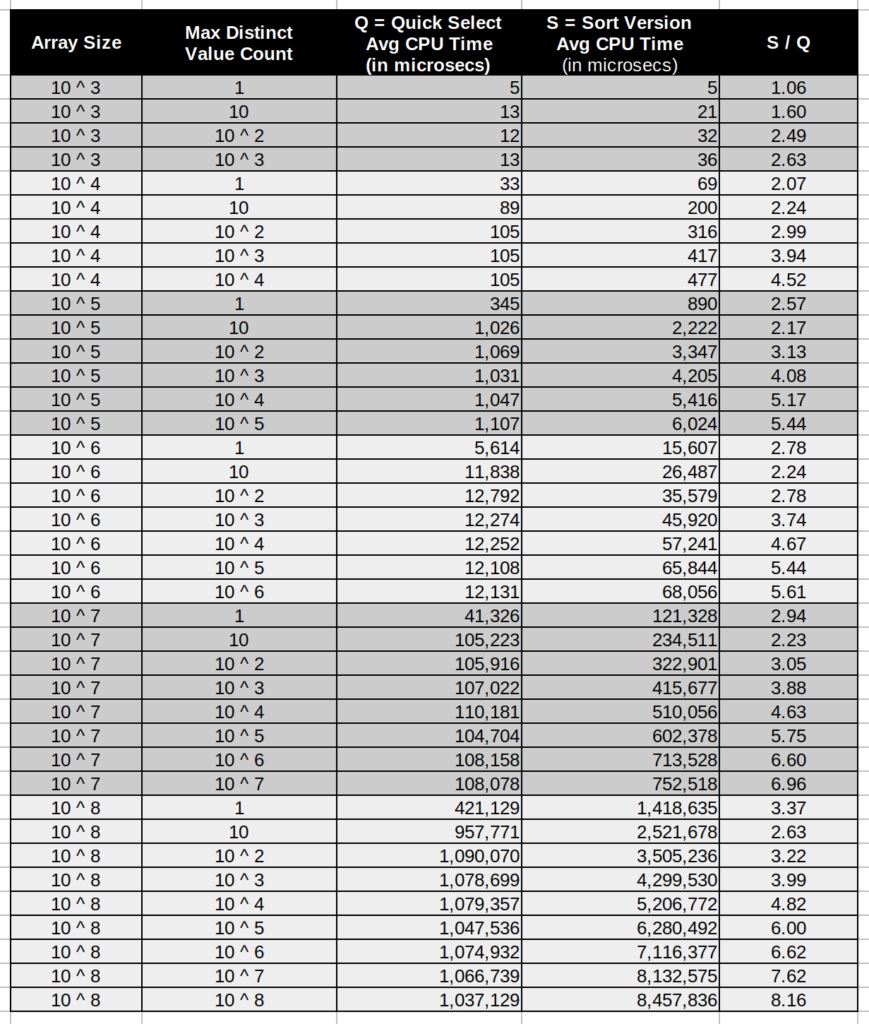
I tried to analyse the performances under broad variance of both array size and max distinct value counts in the array. Below you can find the performance comparison table.
Final Insights
It is clear from both theoretical perspective and analysis results, arguably quick-select is far better than the sort version.
The code above contains further optimizations. For example, if the partition block size is very small, we can apply insertion sort for this block and return the median value, no need to partition this very small block.
Please carefully conduct your own tests before using this implementation. Happy coding. 🙂

