Undirected Graphs – Serhat Giydiren

November 12, 2022

Data Structures & Algorithms

An excerpt from the book Algorithms (4th Edition) by Robert Sedgewick and Kevin Wayne. And I also added a python implementation.

Table of Contents

Definitions

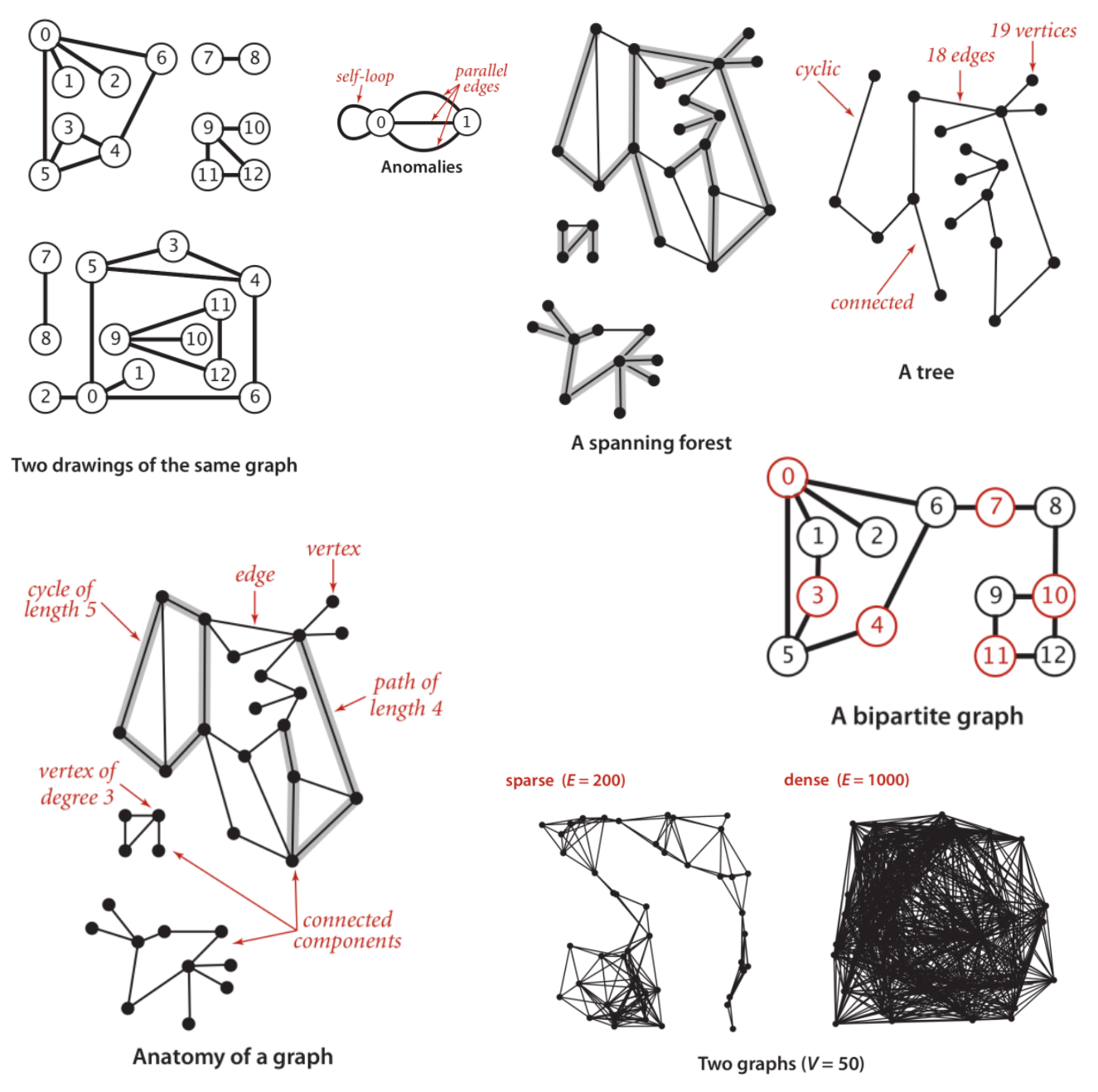
A graph is a set of vertices and a collection of edges that each connect a pair of vertices.
A vertex is the fundamental unit of which graphs are formed.
An edge is a connection between two vertices.
A path in a graph is a sequence of vertices connected by edges.
A simple path is one with no repeated vertices.
A cycle is a path with at least one edge whose first and last vertices are the same.
A simple cycle is a cycle with no repeated edges or vertices (except the requisite repetition of the first and last vertices).
The length of a path or a cycle is its number of edges.
A graph is connected if there is a path from every vertex to every other vertex in the graph.
A graph that is not connected consists of a set of connected components, which are maximal connected subgraphs.
An acyclic graph is a graph with no cycles.
A tree is an acyclic-connected graph.
A disjoint set of trees is called a forest.
A spanning tree of a connected graph is a subgraph that contains all of that graph’s vertices and is a single tree.
A spanning forest of a graph is the union of spanning trees of its connected components.
A self-loop is an edge that connects a vertex to itself.
Two edges that connect the same pair of vertices are parallel.
Mathematicians sometimes refer to graphs with parallel edges as multigraphs and graphs with no parallel edges or self-loops as simple graphs.
When there is an edge connecting two vertices, we say that the vertices are adjacent to one another and that the edge is incident to both vertices.
The degree of a vertex is the number of edges incident to it.
A subgraph is a subset of a graph’s edges (and associated vertices) that constitutes a graph.
The density of a graph is the proportion of possible pairs of vertices that are connected by edges.
A sparse graph has relatively few possible edges present.
A dense graph has relatively few possible edges missing.
A bipartite graph is a graph whose vertices we can divide into two sets such that all edges connect a vertex in one set with a vertex in the other set. You can colour one set of vertices red and the other set of vertices black.

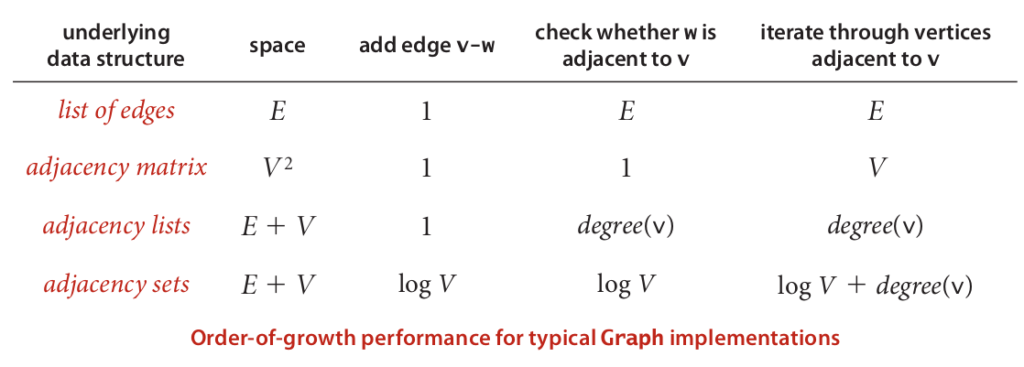
Graph Representation Alternatives

We have 2 basic requirements to choose the best graph representation (data structure) to use.

We must have the space to accommodate the types of graphs that we are likely to encounter in applications.
We want to develop time-efficient implementations of Graph instance methods (the basic methods that we need to develop graph-processing clients).

Adjacency Matrix

We maintain a V-by-V boolean array, with the entry in row v and column w defined to be true if there is an edge adjacent to both vertex v and vertex w in the graph, and to be false otherwise.

This representation fails on the first requirement. Graphs with millions of vertices are common and the space cost for the V² boolean values needed is prohibitive.

Array of Edges

Using an Edge class with two instance variables of type int.

This direct representation is simple but it fails on the second requirement, implementing the get_neighbours function of a vertex would involve examining all the edges in the graph.

Adjacency List

We maintain a vertex-indexed array of lists of the vertices adjacent to each vertex.

This data structure satisfies both requirements for typical applications and is the one we will use here.

This implementation achieves the following performance characteristics:

Space usage proportional to V + E
Constant time to add an edge
Time proportional to the degree of v to iterate through vertices adjacent to v (constant time per adjacent vertex processed)

Python Implementation

Undirected Graph Class

class Graph:
  def __init__(self, V):
    self.__V = V
    self.__E = 0
    self.__adj_list = [[] for i in range(V)]

  def V(self): return self.__V

  def E(self): return self.__E

  def add_edge(self, v1, v2):
    self.__adj_list[v1].append(v2)
    self.__adj_list[v2].append(v1)
    self.__E += 1

  def neighbours(self, v):
    return self.__adj_list[v]

  def __str__(self):
    res = ''
    for v in range(self.__V):
      res += str(v) + ': '
      if self.neighbours(v) is not None: res += str(self.neighbours(v))
      res += '\n'
    return res

Test Client

from undirected_graph import Graph
import requests

def create_graph_from(url):
  response = requests.get(url)
  data = response.text.split('\n')
  v = int(data[0])
  e = int(data[1])
  g = Graph(v)
  for idx in range(e):
    v1, v2 = data[2 + idx].split(' ')
    g.add_edge(int(v1), int(v2))
  return g

g = create_graph_from('https://algs4.cs.princeton.edu/41graph/tinyG.txt')

print(g)